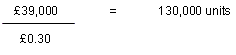Ian McIsaac

Tailored and Public Courses

4

FINANCIAL ANALYSIS

4.4

Break-Even Analysis

Revenue = Costs + Profit (R=C+P)

We can break this down further by recognizing that all costs do not change at the same rate and in the same way. The cost of an increase in productive labour, for example, has no effect on the depreciation cost of a machine, or on the rent paid for the building. However, volume of production (or revenue) is one of the usual causal factors in changing productive labour costs (more revenue may mean you must hire additional staff). The depreciation expense and the rent cost, on the other hand, are fixed with time.

Therefore, costs can be broken down into variable costs (varying according to volume) and fixed costs (which remain constant up to a certain revenue level or given unit of output).

Now, let’s take a second look at our revenue equation:

Revenue = Variable Costs + Fixed Costs + Profits (R=VC+FC+P)

Let us suppose that, in a business producing pots, 70%, or £0.70, out of every sales pound represents the variable cost. Fixed costs are £30,000. £0.30 pence (£1.00 - .70 = .30) out of every sales pound will be left over to contribute to the coverage of the fixed costs and profit. It follows that the number of units that must be sold to break-even would be:

Clearly, any pots sold above the break-even level would mean that the “contribution” would all go to profit, since the fixed costs were already covered.

Now suppose that the company decided to do some additional advertising to stimulate sales revenue, say an additional £9,000. Because advertising is most often a commitment not based on volume, the firm in effect would be increasing its fixed costs by that amount. Thus the fixed costs would now be £39,000. Quite logically this moves the break-even point further out. The contribution remains the same so the new break-even point would be:

This means the company must sell an additional 30,000 pots (130,000 – 100,000) to reach the break-even point and begin making a profit again. So what’s the decision? Well, the manager would have to feel that the additional money spent on promotion would indeed generate more than just 30,000 units before it would be a wise move.

It must be added that we have looked at a quantitative measure for examining alternatives. There may be other factors – qualitative factors – that play a part in your final decision. Even though a certain service in the short run provides a fairly low contribution, you may still decide it is necessary because customers demand it as part of their total package. Break-even/Contribution analysis is often of considerable help in providing additional data for decision-making. After that, it still becomes a matter of managerial judgement.

Analysts may also come across the term operational gearing when they are looking at the cost structure of a company. An activity with relatively high fixed costs to its variable costs is said to have high operational gearing.